WP-A1. Robot motion planning for multiple robots
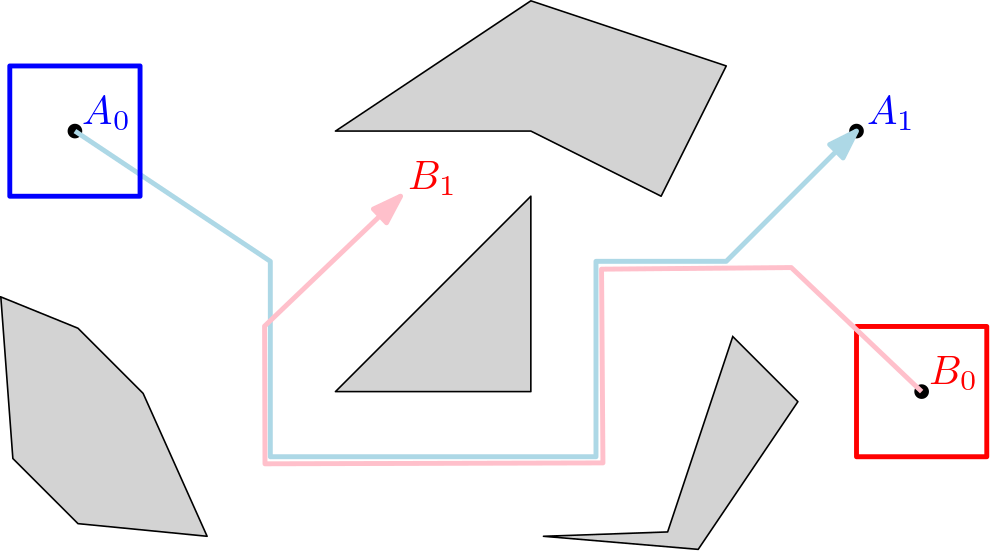
Motion planning is a fundamental problem in robotics: it involves finding a motion to move a robot from a source to a target position. Robots usually have to move amidst obstacles of different types, avoiding obstacles to prevent collisions. The literature in robot motion planning is vast. Robots can have a multitude of different shapes, and different degrees of freedom. Obstacles can also vary, but they are usually assumed to be still. However, when more than one robot moves in the same environment, the robots become moving obstacles to each other, making the problem significantly harder. A motion of a set of robots such that no two robots ever collide is called a coordinated motion. The figure to the right shows an example where two square robots (blue and red) must move from an initial to a final position avoiding obstacles and the other robot. Many variants of coordinated motion planning problems have been studied. Given the high complexity of the motion planning problem, most research has focused on finding motions that avoid all obstacles and whose total length or maximum time needed to finish the motions is close to optimal. In contrast, the goal of this work package is to characterize and produce optimal coordinated robot motions for a small number of robots, i.e., motions that have, for instance, minimum possible total Euclidean length, where two robots need to move from a source to a target position.
WP-A2. Algorithmic analysis of geographic information

One of the main application domains of Computational Geometry is Geographic Information Science (GIS). The reason is simple: all geographic data is geometric, by definition. Despite this, the interaction between Computational Geometry and GIS is still somewhat limited. The overall goal will be to put into value the knowledge about geometric algorithms of the team, by proposing innovative solutions to problems involving geographic data. A strong focus of this package will be on a particular type of geographic data: trajectory data. This is location data generated throughout time by location-aware devices, most
notably GPS. To be able to process large amounts of trajectory data efficiently and to be able to extract meaningful knowledge out of them, many challenges need to be faced. Some examples are computing similarity between different trajectories or clustering them.
WP-A3. Engineering applications of graph coloring

Graph coloring is a widely used mathematical tool that has been applied in different fields of engineering, shown to be especially successful for radio frequency assignment problems. Spectrum graph coloring, recently introduced by members of the team, considers an interference matrix which assigns a weight to each possible pair of colors, so that edges get the weight of their pair of vertices. This generalizes the traditional vertex coloring problem, providing greater flexibility. The aim of this work package is applying spectrum graph coloring to engineering problems where different values of interference arise, for example frequency assignment in Wi-Fi networks. Part of this research line will rely on computational experiments, testing heuristics to obtain good solutions for the inherently hard problems studied.
WP-A4. Computational geometry and collective intelligence for large-scale sensory analysis
Sensory characterization of food is among the most important tools in sensory analysis and consumer science, both in industry and academia. This work package aims to exploit the computational efficiency and easy visualization of geometric techniques as an alternative to statistics for the sensory characterization of products. In order to do so, we propose a pioneer multidisciplinary approach, which involves the three areas of Sensory Analysis, Computational Geometry, and Collective Intelligence. From Computational Geometry, we will study clustering and visualization alternatives, comparing them with the state-of-the-art techniques, implementing different choices, and performing a large number of computational experiments. From Collective Intelligence, we will consider quantitative and qualitative evaluations, asking the tasters to rate and rank both samples and opinions from other consumers, feeding an iterative procedure to get more tuned characterizations of the food samples. From Sensory Analysis, the methods developed will be validated by a sufficient number of tasting sessions of two types, on the one hand using a computational infrastructure to virtually taste images as surrogates of samples, and on the other hand tasting actual samples of foods.
WP-T1. Combinatorial and algorithmic properties of point configurations

Problems about configurations of points are basic in Discrete Geometry and Computational Geometry, since they capture information about positions of objects, complex numbers, or statistical data, among others. The general aim of this research line will be the study of properties of point sets, contributing to a better understanding of their structure and invariants. Some particular problems to be considered include Erdős-Szekeres problems, for which we will study relations between the numbers of polygons of different sizes and generalizations from the usual convexity to the restricted-orientation convexity. For an example, the figure shows the maximum-area empty orthoconvex polygon for a set of points on an axis-aligned rectangle R. Another problem to be considered is counting the number of noncrossing geometric networks that can be drawn on a given point set. Also, we will study other structures like Voronoi diagrams, properties as order types, and random point sets.
WP-T2. Combinatorial and algorithmic properties of geometric networks
Geometric (or Euclidean) networks, whose vertices correspond to points in the plane and whose edges correspond to straight-line segments, are a remarkable object of study in Discrete and Computational Geometry. In particular, an important line of research is network design, whose problems include the optimization of networks according to certain measure or parameter, as well as the study of the impact that changes in the network have over different properties. In this line, we will consider changes like inserting segments or cutting the network in several components by a line. We aim at gaining a deeper understanding of geometric networks, and the optimization of aspects like the diameter, the average distance, or the radius. In addition, other aspects related to distances, proximity parameters, and shortest paths will also be of interest.
WP-T3. Parameters and properties of abstract graphs
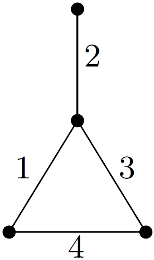
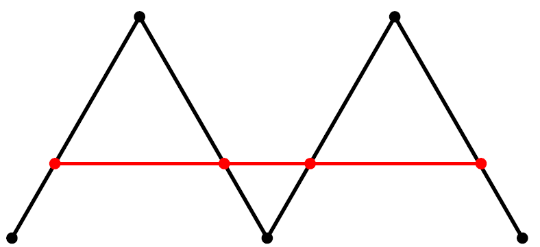
A first goal of this package is the study of different variants of locating and dominating sets of graphs, which can be used to distinguish vertices subject to certain conditions. This type of set plays an important role in the study of networks, like optimally locating a set of sensors in a network to detect the failure of a node. We are interested in solving this kind of problem even if some vertices of the set fail and also in determining sets that simultaneously distinguish several vertices of the graph. We are particularly interested in graph classes commonly used in network architectures, such as cycles, trees and grids, and in planar graphs, because they appear in many problems related to geometrical aspects of a network. We will also study the inverse problem of confusing vertices as a privacy measure. As a natural extension of our study on parameters, we also aim to work on other combinatorial structures, such as the domination polynomial or the Tutte polynomial, whose interest rely on the great amount of information that contain about the associated graph. Another goal is the study of problems related to graph labelings, coding theory, circuit design and communication network addressing. In 1990, Hartsfield and Ringel conjectured that every connected graph of order at least 3 has an antimagic labeling, where the sums of the labels of edges incident to a vertex are pairwise different. See the figure on the right for an example. This conjecture is still open, even for the class of trees and, on the way to prove or disprove this conjecture, we are interested in determining the existence of antimagic labelings for some classes of graphs. We will also work on the oriented chromatic number, for which upper and lower bounds are known for some classes of grids, aiming to find exact values for these graphs, if possible, or to constrain the interval of possible values, otherwise.